A DOGLIKE
PROGRAMMING
BOOK
A Chicken Jerky Flavoured Introduction to
Functional Programming

Juuso Vuorinen
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License (CC BY-SA 4.0)
ISBN 978-952-94-3254-7 (PDF)
ISBN 978-952-94-3255-4 (HTML)
id.)
ISBN 978-952-94-2930-1 (PDF)
ISBN 978-952-9
4-2931-8 (HTML)
Contents
Automatic Data Processing is back. 7
Algorithmic thinking and recipes. 7
Step-by-step instructions with variables. 8
From recipes to data processing machines. 9
Learning math is fun and beneficial 13
Instructions for the reader 13
Building data processing plans cannot be automated. 16
Function as a data processing machine. 16
Raw materials of many kinds. 27
Supplying many raw materials. 27
Typical raw materials of programming. 29
Chapter 4. Numbers as raw material 31
Chapter 5. Characters and strings as arguments. 43
Chapter 6. Pattern matching and chicken jerky treats. 54
Chapter 5. From chicken jerky bags to lists. 57
Lists and list related functions. 57
Lists and pattern matching. 59
Chapter 6. Filter function. 63
Chapter 1. Preface
Automatic Data Processing is back
Programming is considered an important skill in Finnish schools. It was added to the national curriculum two years ago as Finland reformed the national core curricula at all levels of education. Primary school teachers have been provided a variety of training courses on elementary programming. This is especially true of math teachers as math teachers have shown the greatest interest in programming among teachers. A similar development has been seen in many other countries.
Functional programming seems like a good fit to many programming problems. It does not make programming any easier than before, but the approach makes it easier to build and maintain high quality software.
Anyone can learn to write simple programs: imperative, functional or something in between. This book is about solving simple problems with functional programming. Functional programming is not a swiss army knife for solving all programming problems. However, functional programming provides the simplest toolkit of concepts of all programming paradigms. Less is more.
Algorithmic thinking and recipes
Many educators, at least in Finland, highlight the importance of algorithmic thinking as a prerequisite for learning programming. Algorithmic thinking is often represented as steps that results in a program. A food recipe is often used as an analogy to algorithmic thinking. A meal is prepared according to the recipe, one step after another. The process might include repetitive tasks such as preparing of 10 sandwiches. The computer works the same way, it is given instructions which will eventually be executed. Once all the instructions are executed the program finishes – the meal is served.
But there is a problem with the recipe analogy. The analogy emphasizes the inner workings of the computer itself. However, data processing plans are difficult to make if we need to think how computers work. It may sound controversial, but data processing problems are best solved without a computer. Rather than thinking about a bunch of instructions given to the computing machinery, one might consider a data processing plan.
Step-by-step instructions with variables
Mutable variables are not needed in order to understand programming or algorithmic thinking. But very often when we design even the simplest algorithms, the discussion turns to memory and variables. This is when we have already gone way too far towards the physical end of the computing continuum. This happens at the cost of missing the data processing plan, plain and simple.
When we design programs, we do not need to use phrases such as ”storing a number in memory”. We do not need variables when we make our data processing plans. Variables refer to the computing machinery and have nothing to do with the data processing plan itself. The computer is not part of our problem domain and this should show in our data processing plan.
The recipe analogy may work fine for teaching and learning algorithmic thinking as such. But whenever we use phrases such as “we need to store this number”, we refer to the computing machinery. We may even be cheating ourselves. We may not need to store anything. The recipe analogy is a poor match to many programming problems not only because it refers to action descriptions rather than problem declarations, but also because it misses the concept of composition as the key ingredient of any software. As the recipe analogy fails to reflect composition, the analogy simply fails to be the thing analogized.
Should we abandon the recipe analogy as a means to teach or learn programming? The analogy does not seem to reflect the true nature of the problem. Instead of asking “How do we instruct the computer to solve the problem?”, we could ask “What is the data processing plan?”
The recipe analogy with its commands, orders and instructions rhetoric, refers to the computing machinery. This results in a mixture of concepts, some referring to the computing machinery, others referring to the domain logic. It is like a bowl of something, but no one really knows what’s in it. How does the recipe analogy fit into the challenges such as the gathering of data from a number of data sources? Answer: Not very well.
We would be better off with data processing plans, but still tend to emphasize more or less separate steps at the cost of not reaching the simplest representation of the problem. We turn on the oven, mix the ingredients, wait for the oven to warm to 200 degrees and so on. The recipe analogy neglects the fact that data processing related problem solving is at its best when the problem can be depicted as such, not instructing the computer on how it should execute to get the problem solved.
The quality of the software does not depend on the programming paradigm chosen, but on how different paradigms are applied to the current problem. If educators emphasize imperative programming at the expense of functional programming, one can never pick the right tool for the job as the conceptual toolkit is missing tools.
From recipes to data processing machines
Instead of the recipe analogy, we could use the machine analogy. A machine gets some input to work on and it produces some output. The inputs and outputs are data. There we have it, a data processing machine.
Programming is often about making data processing plans, which are composed of data processing machines.
Function machines have been used for teaching high school students the basics of functions. It could be a suitable analogy for introducing functional programming, too.
We know from chef competitions, that chef’s mood can have a great effect on chef’s performance. The chef might have thrown a party the night before the competition and he is tired and headachy in the competition. Chef’s tiredness affects his ability to perform.
There is no state to functional programming. To put it bluntly, because there is no mutable state, there is neither headache nor tiredness.
”Side by side…”
If we need to express things running in parallel, it makes sense to equate programming with an input/output system. What happens if we add a second machine next to the first one in our factory? The productivity of the factory is likely to increase by 100%. We expect to get more things done in the same time.
What if we hired a new cook and now had 2 cooks instead of 1 working the busy afternoon shift in our restaurant? Would we get a 100% increase in productivity? Every cook is different. The fresh hire may have a hangover when he starts his shift. Also, the cooks may need to share an oven or hotplates – the productivity may not increase by 100% when the second cook enters the kitchen. There can only be one frying pan on one hotplate at a time.
The factory can be added new production lines with new machines, parallel to the old ones. A machine that is fed with the same raw materials, always produces the same output. Machines do not suffer from hangovers or share resources other than energy that runs them, and therefore the output is directly proportional to the number of machines.
Software representations of parallel computations have become more important as computers have evolved to do more things at the same time. Modern computers are like factories with many production lines. We should learn to design programs that best suit the devices that run them.
Emphasizing parallelism in the preface of the book may sound like geekery, but it is not. Computers with many production lines are very common and this should be highlighted in the curricula, too.
Paradigms matter
Programming paradigms matter. Imperative programming paradigm is the right choice for building software that controls hardware. The paradigm may also be a good fit, if we need to optimize performance. A vast majority of software developers do not need to optimize performance nor control hardware.
We should be able to write programs to be simple yet expressive. By looking at the code we should be able to pinpoint the data processing plan. If we want to build easy to understand data processing plans, our choice of style is functional. Functional programming style is the easiest way to represent understandable yet robust data processing plans.
In an imperative language, sets are often manipulated by a loop. The same construct of loop is used for different problems. The code is difficult to understand, because it does not represent the problem. One of the virtues of functional programming is the use of higher order functions such as map, filter and reduce.
Each function solves a different problem. This shows in the code and the code becomes easier to understand. A person who thinks imperatively, instructs the computer. A person who thinks functionally, represents the problem.
Dealing with sets is fundamental to many programming languages. The concept of looping hides the transformational nature of the activity whether it is filtering, mapping, reducing or something else. A loop does not give the reader a hint about the type of the transformation either. This is one of the reasons why imperative code is harder to understand than functional code. The picture below illustrates this.
Picture 1. Imperative and functional programming.
The readability of the code affects the cost of development and maintenance of any information system. If the code is difficult to understand, it is also difficult to modify and further develop.
The advent of cloud computing has made serverless computing an excellent domain for functional programming. A persistence solution, such as a relational database, and functions live in two separate worlds. State management is often hidden from the software designer and one can concentrate on designing the data processing plan. Yet, the software itself can be divided into pure functional and less pure parts, which further helps to maintain and test the software.
The purpose of the book is neither understate imperative programming nor exaggerate the virtues of functional programming. The author of the book understands, at least to some extent, the sins and virtues of both paradigms. There will be trouble, if a paradigm is applied to a problem it does not fit. The book helps you to build simple data processing plans.
Learning math is fun and beneficial
Functional programming supports the learning of math. Functional programming is the best way to learn programming and math at the same time. This is because functional programming is mathematical in nature – it is based on functions.
However, there are many functional programming languages. For learning math, we should choose the language that best suits our objective. Haskell is a perfect language for learning both, programming and math. Selma and I can assure you that the only side effect of learning Haskell is that you learn math for free.
Instructions for the reader
Haskell helps us to keep the data processing plan simple. A Haskell program is a bunch of expressions or functions that are evaluated when the values of the expressions are needed. Language constructs are based on math.
The book will guide you to functional programming along with Selma and her friend Pate. Selma and her friend will show that functional programming in Haskell is not only fun, but also challenging. We hope that this book inspires you to explore functional programming.
The book seeks to guide the reader to the functional way of thinking with simple examples. To begin with we introduce you to the sort function. We use sort as an example of a function that transforms data.
We continue by introducing functions that consume and produce numbers. In the first half of the book the term function will often be replaced by the term machine. Also, the term argument(s) will often be replaced by the term raw material or input. Also, the term value, that refers to the evaluation result of a function, is often replaced by the term output.
Then we play with functions that take characters as input. We learn to compare things. We make it clear to the reader that machines need other machines to solve more complicated data processing problems. We emphasize the importance of the interplay between any two machines. The output of one machine is the raw material (input) of another machine. In the end, there will be a chain of connected machines, like a production line of a factory.
The reader is also introduced strings. Strings are also used to demonstrate machines that produce outputs other than numbers, like other strings and truth values. We introduce characters and strings at the beginning of the book, because they allow us to build simple, yet somewhat meaningful programs.
Pattern matching is only introduced on the surface. Had we omitted pattern matching altogether, many readers would have been left with no means to follow many online resources with Haskell code examples. This is because many code examples are based on pattern matching. Pattern matching is such a fundamental part of not only Haskell, but also many other modern programming languages, that it cannot be completely ignored even in an introductory book like this.
The rest of the book is devoted to designing data processing plans for list type data with higher order functions map, filter and fold. The list is among the most important, if not the most important data structure in programming. List transformation examples become more difficult towards the end of the book. The fold function will be introduced at the end of the book, as it is the most challenging of the three. Also, we get introduced to a custom data type, but do not go into the Haskell type system.
The higher order functions should be studied from the simplest to the more complicated. Start with the filter function. Then look at the map function. And lastly, consider the problems that could be solved with the fold function. By combining these functions, you can solve almost any problem.
The concept of recursion or the type system of Haskell are left out deliberately. Understanding recursion is not a prerequisite for learning functional programming. The user of a higher order function is often using a recursive function under the hood.
The user of a higher order function does not benefit a great deal for being aware of recursion as a repeat mechanism. Functional programming languages often have functions that are based on recursion, but this does not show too much on the programming interface.
However, being aware of the recursive nature of a function can be useful. Such awareness is useful, for example, in situations where a performance problem is hit or execution stack flows over. Having read this book, a theoretically oriented reader might wade through recursion. A more pragmatic reader would use the higher order functions as such and would not pay too much attention to the implementation details of the language.
In the code examples of the book, > indicates that we should type that line. => indicates that Haskell interpreter prints that line.
This book is inspired by Bartosz Milewski’s book Category Theory for Programmers.
Have fun programming!
Helsinki, April 12, 2020
Juuso Vuorinen
Canines as well as humans make a lot of mistakes, and sometimes even learn from them. It would be nice if you could email comments and suggestions to further develop this book to the author at juuso.vuorinen@ideallearning.fi.
Chapter 2. Machines
Building data processing plans cannot be automated
The knowledge of how to process data is probably one of the most fundamental skill of any programmer. In order to work with data, we need a bunch of concepts to base our data processing machines on.
Our data processing plan is not created out of thin air. To come up with a data processing plan is something we cannot automate. In order to process data, we must define how new data or information is generated from the data or information we already have. This process is somewhat analogous to designing production lines of machines within a factory.
Function as a data processing machine
We can also replace the term machine with the term function. It is characteristic of a function that if we want to get a value from the function (a thing produced by a machine), we have to give the function an argument (raw materials fed to the machine).
The concept of function is a suitable building block for representing data processing. The concept of function abstracts away the physical computing machinery, yet it is concrete enough for building unambiguous and easy to understand data processing plans.
If we compare the functional and imperative approaches, we find that the functional approach with machines is better suited for not only solving data processing problems, but also representing data processing problems. The difference is somewhat the same as between Arabic numbers and tally marks.
A lumberjack can resort to tally marks and manage his accounts without Arabic numerals, because he is too lazy to learn them. If the lumberjack takes his accounts to an accountant who only understands Arabic numerals, it may prove difficult to set up the accounts.
When an accountant tries to interpret the tally marks of lumberjack’s accounts, he first adds up the bundles of five. The accountant must then add the sum of the remaining tally marks to the bundles of five. The accountant may need to add up many subsums and finally write down the total in Arabic numerals.
When adding up the bundles of five, the accountant can accidentally skip a bundle or add an extra bundle. Also, if the last bundle does not contain five marks (four vertical and one diagonal slash), the accountant may accidentally skip a mark or add an extra mark. Counting slashes that are close to each other is cumbersome and error prone.
To allow a mild exaggeration, we can say that those who prefer functional style use Arabic numerals, whereas those who fancy imperative paradigm, rely on tally marks. All the above assuming functional solution would suite the programming problem at hand. Tally marks are easier to learn than Arabic numerals. Yet it is difficult to imagine the World being run by tally marks.
It is certainly difficult to describe the differences between imperative and functional programming paradigms in one sentence, and the exaggeration does not do justice to either of the paradigms. The purpose of the tally mark example is to give the reader an idea of the nature of the differences between the two paradigms. Now, let’s give the floor to Selma and Pate and start exploring our first machine, the sort function.
Our first machine
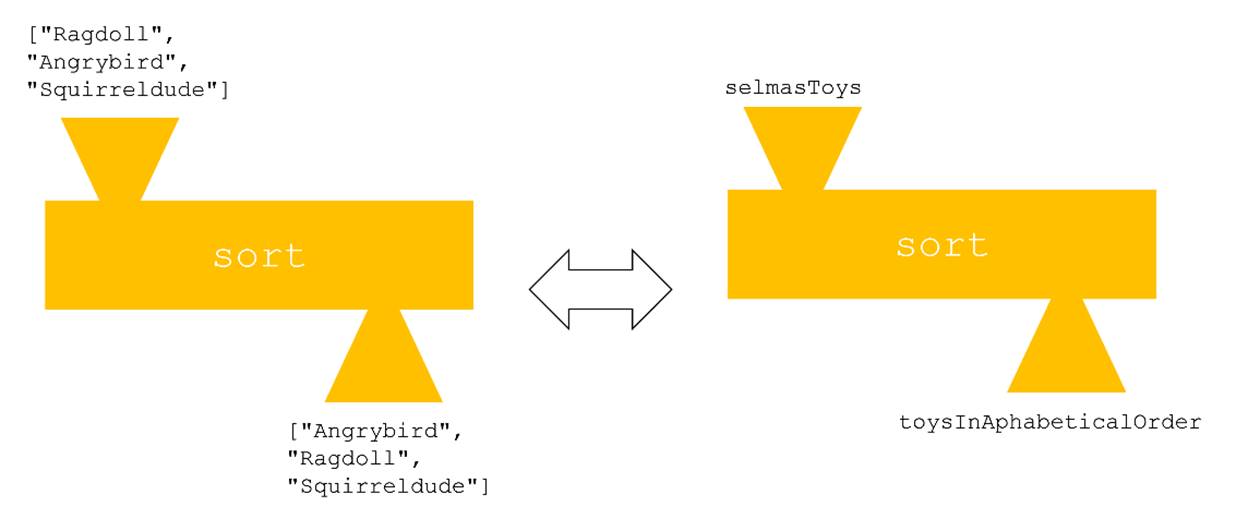
”Pate, let’s look at the picture and code of the sort machine”, says Selma. ”With this piece of code I can sort my favourite toys in alphabetical order”
Picture 2. Two ways to use the sort machine
1 import Data.List.sort
2 selmasToys = [”Ragdoll”,”Angrybird”,”Squirreldude”]
3 toysInAphabeticalOrder = sort selmasToys
”What do these pictures mean?” asks Pate.
”Wait, and I will tell you”, replies Selma. ”On the left side of the horizontal two way arrow we feed the raw material to the machine as such, on the right side of the two way arrow we feed the raw material to the machine by referring to their names.”
”Oh well, what does that code mean then?” asks Pate curiously.
“Let me explain”, says Selma. ”The first row reveals that we want to use a machine (function) sort, which can sort a list of words into alphabetical order. If there are already machines that can do what we want, we should use them instead of building our own from the ground up. Sort is an example of such a machine. To use the machine, we need to import the machine to our program. We use the import keyword to tell the system that we want to use a machine external to our program. After the import keyword comes the so called fully qualified name of the machine such as Data.List.sort. We do not need to worry about the meaning of the term fully qualified name at this stage.
We can think that we have two separate machines, one in the second line and another one on the third line. On the second line, a machine (function) on the right side of the equal sign produces a list of items from the items fed to it by listing them one by one and enclosing them in brackets. On the third line, a machine (function) on the right side of the equal sign produces an ordered list from the items that were produced by the first machine on the second line.
On the second line we define a list that contains three items, my favourite toys. As you see, the list items are separated by commas and enclosed in brackets. Items are also enclosed in quotation marks. What do you think Pate? Does this make any sense? ” asks Selma.
”I just don’t get it”, says Pate. ”Why are the machines on the second and third line on the right side of the equal sign so different, even though they are both machines? I understand the code on the third line. We feed the sort machine with a list of words and then we just wait until someone turns the machine on. But where is the machine (function) on the second line? I can only see a bunch of words enclosed in brackets, each word enclosed in quotation marks and separated by commas like this [”Ragdoll”, ”Angrybird”,”Squirreldude”]. I would expect to see a machine named createList or equivalent. Where is it hiding?” asks Pate.
”Let me explain”, says Selma. ”We just said that the name selmasToys represents a list that contains all the toys as listed in the first line of code. Still, we do not see a named machine on the right side of the equal sign in the first line of code such as createList. What is this all about? Have I been cheating on you Pate? No, I haven’t. The brackets and commas represent a machine that creates a list out of the listed items.
On the right side of the equal sign is a machine or the name of a machine. On the left side of the equal sign there is always the name of a machine.
The names of the toys enclosed in quotation marks are the raw material fed to the machine that creates the list. Therefore, the right side of the equal sign is indeed a machine, and the left side of the equal sign is a shorter representation of the machine, the name of the machine. Remember, it is sometimes difficult to see if something is a machine or not. Brackets are a good example of this. Brackets and commas represent a machine to create lists. There is more to it than just brackets and commas, but for now we are satisfied with this explanation.
There is one more question I would like to ask you. What would happen if you wrote x = x on the Haskell interpreter and then started the machine by entering x and pressed return on the keyboard?”
”That is a tough question Selma. Let me think a moment… If we write x on the Haskell interpreter, a machine named x should be started. The machine starts again the machine named x. This leads to the same machine being started forever. Could it be that the machine runs forever and does not produce anything, but just keeps starting itself again and again. So, we keep starting the machine until the end of the World?”
”Good Pate!” says Selma. ”That’s what will happen. The machine does not really produce anything sensible, but still runs forever. Let’s give it a go:
> x = x
> x
You can now stop the program by pressing ctrl + c in order to continue your programming exercises. It may feel strange to run a program that just keeps going. We will get back to this later. But before that, you deserve a chicken jerky now that you have boldly gone where no dog has gone before and started a machine that runs forever.”
Production lines
A Haskell function is a smart machine since it starts only, if another machine (function) needs its output. A machine’s need for some raw material (input) ends up another machine getting started to produce the raw material (output). The raw material can also be produced in code, such as listing Selma’s favourite toys. The output of one machine is the input of another machine. The machine (function) never produces anything in stock, because it is only started when its products are needed by some other machines (functions). We do not need to store anything.
We can say that selmasToys is the name of a machine. The name selmasToys produces a list of Selma’s favourite toys. In the code below, we can see how the name selmasToys has been replaced by the machine itself, with brackets, commas, double quotes around the words, and all. After the name sort, we find the original list of Selma’s favourite toys as such. It is important to understand that machine’s name can always be replaced by the machine that the name represents. That’s why the code below produces the same output as the code we saw before.
1 import Data.List
2 toysInAphabeticalOrder = sort [”Ragdoll”,”Angrybird”,”Squirreldude”]
> toysInAphabeticalOrder
=> [”Angrybird”,”Ragdoll”,”Squirreldude”]
A name on the left side of the equal sign is a shorter way to express a piece of code on the right side of the equal sign. Selma thinks that it is not too smart to repeat the list of three items everywhere, but use the name selmasToys instead of [”Ragdoll”,”Angrybird”,”Squirreldude”].Let’s get back to exploring the piece of code that we were introduced to in the first place:
1 import Data.List.sort
2 selmasToys = [”Ragdoll”,”Angrybird”,”Squirreldude”]
3 toysInAphabeticalOrder = sort selmasToys
> toysInAphabeticalOrder
=> [”Angrybird”,”Ragdoll”,”Squirreldude”]
”Writing this small program and then writing the name of the machine (function) toysInAphabeticalOrder on the Haskell interpreter and pressing the return key we end up starting at least two machines”, Selma explains. ”Can you guess Pate what are the machines that get started and in what order?” asks Selma.
”I sure can guess and maybe even know”, says Pate. ”The first machine to start is obviously the machine that creates the list with the name selmasToys. Once the list has been created, it is fed to the sort machine, which in turn creates a new ordered list with the name toysInAphabeticalOrder. The content of which we see on the Haskell interpreter following the => sign.
So, we need to go to the beginning of the production line and create the initial list. We need the initial list for the sort machine to transform the initial list into a new, ordered list. This is easy peasy for an Irish wheaten terrier like me”, says Pate.
”Exactly!” says Selma. ”You are about to become a functional programming wizard”, says Selma.
”I may not qualify as a wizard quite yet, but maybe in a month or two I can use the terms properly and maybe I am able write simple programs. By the way, what would happen if I wrote selmasToys on the Haskell interpreter and pressed the return key?” asks Pate.
”What do you think?” says Selma.
”Well, eh… maybe the name selmasToys would start the machine that would create the original list. There is an easy way to find out. Let’s try and see”, says Pate.
> selmasToys
=> [”Ragdoll”,”Angrybird”,”Squirreldude”]
”That was no big deal”, says Pate. ”I wrote the name selmasToys and pressed the return key. This really works!” says Pate.
”Is programming really as simple as depicting the machines as such and then connecting the machines?” asks Pate.
”Yes, it sure is. That is fine and doggy enough definition of programming”, says Selma. ”It is something Irish wheaten terriers and crossbreeds of bichon frisé and poodle can easily digest. It is as simple as a marrowbone”, says Selma.
Not how, but what
”There is one more thing I would like you to pay attention. When we design data processing machines, we do not care whether our machines run on electricity or gasoline. Instead, we do care of the kind of raw materials our machines use and the kind of outputs they produce. If you pay attention to these two things, you are likely to learn skills that enable you to define the most beautiful data processing machines ever”, says Selma.
Our dog friends have made quite an effort in learning some basic terms of functional programming. The third line of the first code example reveals the very nature of functional programming.
Selma is not paying any attention to what might happen in the computer’s memory when the initial list of toys is being transformed into a new list of toys. Instead, Selma is only keen on getting the toys in alphabetical order. Even if Selma browsed the source code of the sort machine, she could not see anything that would refer to the manipulating of computer’s memory. When the list is being sorted, we don’t need to worry about how the computer sorts things out. Sort machine is fed with a list as input and it produces another list as output.
The third line of code is in a way similar to the second line of code. On the left side of the equal sign we write a name which is used to shorten the right side of the equal sign. Selma can now shorten the right side of the equal sign to a single name toysInAphabeticalOrder. When we write toysInAphabeticalOrder on the Haskell interpreter, we see the output of the machine, a list in alphabetical order:
> toysInAphabeticalOrder
=> [”Angrybird”,”Ragdoll”,”Squirreldude”]
Running the machines
As we have learnt, machines have inputs and outputs. In order to produce something, we need to do something with the raw material that was fed to the machine. This is called the starting of the machine. As we know, a machine is only started when its output is needed. Pate can ask the Haskell interpreter to find out what is the sorted representation of selmasToys by writing toysInAphabeticalOrder on the Haskell interpreter, after which we see the list in alphabetical order. Starting one machine by its name will typically end up a bunch of machines getting started, not just one. We can imagine a production line where machines consume something which is produced by other machines and produce something to be used by other machines. Machines get and give.
”Let me tell you something Pate. It only makes sense to start a machine, if there is another machine that needs the output of the machine. The same applies to chicken jerky treat manufacturing. The smartest of the chicken jerky treat manufacturers would only manufacture a chicken jerky treat or treats, if we placed an order for them. And we certainly keep placing the orders and there will be business for chicken jerky manufactures. But notice, there is no stock for chicken jerky treats in our Haskell style manufacturing plant”, says Selma.
”From now on, we call our machines lazy, as they will only start if another machine needs their output. It is a just-in-time production line with no stock. Laziness is a virtue, at least on a hot summer day like this”, says Selma.
When we start the machine to transform the original list of toys into an alphabetically sorted list of toys, the alphabetically sorted list will be the output of our production line. The name toysInAlphabeticalOrder on the left side of the equal sign is a shorter representation of the transformation from the original list to the sorted list. When we write toysInAlphabeticalOrder on the Haskell interpreter and press the return key, we start our two-machine production line.
When the Haskell interpreter is fed with toysInAlphabeticalOrder it needs to start a machine named toysInAlphabeticalOrder to produce an output. In order to produce the output, it needs to start the machine named selmasToys first. This is because toysInAlphabeticalOrder needs the output of selmasToys. A machine named toysInAlphabeticalOrder is said to depend on another machine named selmasToys.
Shortly, we create an output from the original list of toys. Then the output will be fed to the sort machine, which in turn produces a new, alphabetically sorted list.
Sort machine knows how to put things in order. That is the capability of the sort machine. We just need to feed it with the original list to get the list transformed into a new, alphabetically sorted one. We can think that the sort machine uses a bunch of other machines under the hood. It is the cooperation of the machines under the hood that enables the original list to be transformed into a new, alphabetically sorted one.
The quality of the input or the quality of the output does not reveal the internals of the machine. The quality of the input and the quality of the output reveal only two things about the machine. The kind of raw material the machine consumes and the kind of output it produces.
Wood is the raw material of the pulp machine, and cellulose produced by the pulp machine is in turn the raw material of the paper machine. If we combine the pulp machine with the paper machine, we get a paper mill that consumes wood and produces paper. We have a production line.
I think we are now aware of the basic concepts of data processing machines. The concepts are machine, input (raw material), output (something produced) and starting of the machine. With these concepts we can build the kind of data processing production lines we want.
In the next chapter we will take a closer look at the input of the machine and explore how raw material flows into the machine. In programming terms, we will get to know arguments in more detail. In the end of the chapter we find ourselves creating more complicated machines to solve more complicated problems.
Chapter 3. Raw materials
Raw materials of many kinds
”As you noticed Pate, the raw material fed to the sort machine is a list. It is a list since we enclosed the items in brackets and separated the items with commas. The raw material of type list is created by a machine. The brackets and commas represent a machine that produces the list.
Like we pointed out earlier, the raw material can also be called an argument. Sometimes our production line is such that we need many raw materials. If the output of our machine is a sum of two numbers, it must be fed with these numbers. The principle is the same as with the sort machine when it is fed with a list of toys.”
Supplying many raw materials
”But hey!” says Pate. “Do you mean that we could feed the different raw materials to a function by using a list to carry the items? Then it would be easy to feed any machine with as many raw materials as we would like. If we wanted to add two numbers, we could simply feed the machine with a list of two numbers, is that right?” says Pate.
”The idea sounds good, and we could make it work. We would only need to make sure that the numbers were of the same type. We could not have a decimal number and an integer in the same list”, says Selma. ”A list can only represent elements of the same type. A list represents either names of toys or integral numbers but never both. The same list cannot have items such as “Squirreldude” and 23. Do you now understand why the different types of raw materials cannot always be fed to a machine with only one list?” asks Selma.
”I see”, says Pate. “It is the same as with a shopping list. A shopping list only contains the stuff that we are about to buy, not things like vehicle registration numbers, bus timetables or the phone numbers of our friends. If we want to build a machine that is fed with two different raw materials such as one number and one word, we need two pipes to feed two different things to the machine. Now I am getting it”, says Pate.
“Yes. You have understood it perfectly Pate”, replies Selma.
“We can feed our machines with different kinds of raw materials. The raw materials could be singular such as a number or a name of a toy from Selma’s list of toys. The raw material could also be a list as we have seen. We can use a list to feed a machine with many raw materials of the same type. But we can also feed the machine with many raw materials of the same type. The type of raw material is defined by the machine to which we are feeding the raw material”, says Selma.
”Aah…”, says Pate. ”So, if we would like to calculate the mean of, let’s say, ten numbers, we would need to feed the meanCalculationMachine with a list of ten numbers.
We could also design the meanCalculationMachine to deal with ten numbers instead of one list. However, this would leave us with a problem. What would happen if we fed the meanCalculationMachine with eleven numbers? We would be in trouble because the machine could only handle ten numbers. We would then need to build another machine that could handle eleven numbers and so on. Am I on the right track?” asks Pate.
”Absolutely”, says Selma. ”We need to pay attention to the types of our raw materials, and think carefully the kind of pipes we use in our factory to feed the raw materials to our machines. For a concrete manufacturing machine there should be one pipe that would transport water, another pipe that would transport sand and a third pipe that would transport cement. The machine cannot be fed with sand and water in the same pipe as this might block the pipe. The same goes for feeding the machine with cement and water in the same pipe. If the production was interrupted, our pipes would be blocked, at least the one with cement in it. Each raw material needs its own pipe”, says Selma.
“Isn’t programming interesting! It is like planning of factories and machines all day long. If I were to build a concrete manufacturing machine, I would choose shiny chrome plated pipes. It would look just awesome”, says Pate.
Typical raw materials of programming
”What type of raw materials are typical in programming?” asks Pate.
”Well, quite often there is a need for numbers and some kind of text, such as the names of Selma’s toys”, says Selma. “Sometimes we may need things like decimal numbers or even fractions. In addition, we are likely to need the so-called truth type, too. Truth type can be used to represent two things, True and False
A set of different elements is called the type. True and False are the different elements of the truth type. Also, types are given names. The official name of the truth type is Boolean. Types are something very typical of many programming languages.
Programmer defined types are very common even in moderately small programs. These types can be used to depict all sorts of things such as cars, balloons, colours, smell, people or anything we like. We need to read the requirements specification and define our own types accordingly”, finishes Selma.
”Why wouldn’t we learn how to define a balloon type? There is nothing more fun than barking at balloons, big and small. The funniest thing about balloons is that they can be charged with static electricity. This can untangle the hair of even the most tangled husky”, says Pate.
”Defining types of our own is fun and useful, too. You can learn the basics of functional programming without not knowing too much about types and how to define them. Having just said what I said, I admit that there is much more to the types than really meets the eye. Types and how to deal with them is like a huge bowl of chicken jerky treaty, tasty and waiting for the hungry explorer. Also, types are important because if you are to become a programmer yourself, you sooner rather than later need to define your own types.”
”Ok! I am satisfied with this explanation for now”, says Pate thinking how he could represent balloons with his very own balloon type.
Chapter 4. Numbers as raw material
”Integral numbers or integers in short, come in many types. A sequence of integers could continue to infinity or a set of integral numbers could be limited and have a negative minimum and a positive maximum”, says Selma.
”It is characteristic of integers that we can use them as raw material, and feed them to our machines. For example. We can feed two integers to a machine that can add two numbers together. First, we write the name of the machine which in case of adding two numbers together is +. Then we need to put the name of the machine in parenthesis (+) and add the raw materials one-by-one and empty space between them.
>(+) 2 3
=> 5
The structure is the same as with the sort machine. First comes the name of the machine and then the raw materials:
> sort selmanLelut
In this case, the name of the machine happens to be + and not a word such as sort. There is another difference between the two. The sort machine is fed with a list and + machine is fed with two numbers. The machines are fed with different raw materials.
When we wanted to sort the list of toys, we did it like this
> sort selmasToys
We can think that selmasToys is a name of the machine. We can also think that 2 is a name for a machine that produces 2. So, we can think that symbol 2 represents something that produces 2 when the machine and its output is needed. So, we can say that 2 represents a machine because it produces something when the machine runs.”
”How can we know that selmasToys means something which is of type list and not something else? The machine name selmasToys does not reveal anything about the structure of the output we get when we use the name selmasToys in our code. We do not see any brackets or other characteristics that would refer to a list. How does this really work?”, asks Pate.
“Well, that’s quite a question Pate. The short answer is this. The smart tools that ship with a programming language can infer the types. Every now and then when we are writing our code, we ask the tools to check that our code is in good shape. Before any of the machines get started, the tools have already figured out that selmasToys is such raw material that it fits with the sort machine. The long answer would be so long that we would need to get back to it in another book.”
”Could numbers 2 and 3 also be replaced by some names that would mean some numbers? Is it so that any names would do, if they meant numbers?” asks Pate.
”Exactly!” says Selma. ”We can define two numbers named firstNumber and secondNumber and replace the numbers 2 and 3 by firstNumber and secondNumber. Look here Pate.”
> firsNumber = (-) 5 2
> secondNumber = (*) 5 4
> (+) firstNumber secondNumber
=> 23
”And listen Pate. It makes no difference how many machines need to be started before firstNumber and secondNumber actually produce the numbers, that are fed to the + machine. Notice that firstNumber and secondNumber mean two things. Firstly, they refer to a machine. Secondly, they refer to the output of the machine. They have two meanings. It would do no harm, if we named them firstNumberMachine and secondNumberMachine, because that’s what they are, too.
The second point I want to make is that, if our machines get fed with the raw materials that fit the machine, we are safe. In the example above firstNumber is the output of the subtraction machine (-) and secondNumber is the output of the multiplication machine (*). Because the output of the multiplication machine and the output of the subtraction machine are both numbers, they can be fed to the (+) machine, too. Isn’t it great! As the types match, there will be a steady flow of raw materials into the machines and steady flow of outputs, too.”
> addingMachine = (+) firstNumber secondNumber
> addingMachine
=> 23
”Wow!” says Pate.
”What I find especially interesting is how we could get the addingMachine’s output fed to another machine for further processing. I wonder how we could further design the program in such a way that the output of the addingMachine could be fed to another machine that could deal with numbers.
How could we feed the output of the addingMachine to the machine that would multiply the raw material by two? We like to reuse the multiply by two machine in our program and therefore give it a name such as doubleMachine. Makes sense, doesn’t it. If you told me how such a machine could be designed, I would buy you an ice cream in the evening. How is that for a deal?” says Pate.
”You got a deal, Pate. This is how we would write the code. Look!
> doubleMachine = (*2) addingMachine
> doubleMachine
=> 46
doubleMachine is the name that we can use to double the output produced by addingMachine.
addingMachine is the name that we can use to add together the outputs that are produced by firstNumber and secondNumber.
firstNumber is a name and it means machine (-) 5 2.
secondNumber is a name and it means machine (*) 5 4.
”And listen to this Pate. There is an order to when the machines run. It is called the evaluation order. When you enter doubleMachine on the Haskell interpreter and press the return key, the machines are started. First, we need to run firstNumber and secondNumber machines, because their outputs are needed by the addingMachine. In the next phase addingMachine is run and it is fed with the outputs of firstNumber and secondNumber. Finally, doubleMachine is run and it is fed with the output of the addingMachine”, finishes Selma.
”So, is the running of machines, and actually the running of the whole program some kind of process where we do our best to figure out the outputs of each machine, and then feed the outputs as inputs to the next machine of the production line and so on until we reach the last output and the program ends?” asks Pate curiously.
”That’s exactly how it works. Brilliant!” says Selma. “When an output of one machine is passed as an input to another machine, we need to be careful with types. If there is a machine that expects water and it is fed with sand, the machine is likely to brake. Therefore, we need to think carefully what goes into the machines and what comes out of them. This is because our program (factory) is composed of different machines (functions) that need to fit together. Remember that one machine’s output is another machine’s input!
Now it is time for some magic. Notice that for some machines the names of the machines can sometimes be added between the raw materials. This applies to + machine, too.
> 2+3
=> 5
This makes the code easier to understand as many programmers are used to adding two numbers together like 2+3 instead of (+) 2 3.
Integers are good raw material to be fed to division and multiplication machines. Integers are also a good match with the machines that simply change the sign of the number. Negative numbers become positive numbers and positives numbers become negative numbers. Does this make sense to you Pate?”
”Yes. Almost everything so far makes sense. There is one thing that I do not quite understand. It looks as if we can use doubleMachine in such a way only that the raw material is always going to be the same, the addingMachine. Wouldn’t it make more sense to design the doubleMachine is a way that it could be fed raw material other than that produced by the addingMachine?”
”Now you are really getting to the point Pate. We sure can, and it is easy. This is how it goes”, says Selma.
> doubleMachine = (*2)
> doubleMachine 5
=> 10
”So, what does that mean and how does it work?”, asks Pate.
”It works exactly like all the other machines so far. Look! Our multiply by two -machine aka doubleMachine is fed with 5 as a second piece of raw material from the Haskell interpreter. It already has the first piece of raw material, which was fed to it in the previous line, namely number 2 right after the name of the multiplication machine, *. Once it is fed enough raw materials for multiplying two numbers, the machine can be started it and produces 10. It needs the other multiplicand and then it is free to produce an output. We remove the addingMachine from the code, and then we have a free slot for our own argument.
Because Haskell is such a lazy language, it only produces output when the output is needed and often eventually fed to another machine as input. When we write doubleMachine and press the return key on the Haskell interpreter, we force the Haskell interpreter to produce the output. The output is not really needed because it is not fed to any other machine. However, the output is produced because the Haskell interpreter wants to show us the output. So, there we have it, the need for the output.
From what we know about machines and production lines, we can say that the setup of machines depends on what we want to produce. Machines could be replaced by functions. This would mean that we would also need to replace the term raw material with the term argument and replace the term output with the term value. If we did all the above replacements of terms, we would be able to compose a perfect data processing production line with a functional language such as Haskell. We would just need to either pick the right machines for the job from the stock of machines or define our own and finally line them up. That would be our production line.
We have now reached a stage where we can forget about the machines and replace them with functions. Also, we no longer need to use the term raw material. From this point on our functions are fed with arguments. What do you think Pate? Does this make sense?”
”Yes, it does. I understand the relationship between the raw material and the machine, and I feel confident if they are replaced with the right terms”, replies Pate.
”Let’s define a new function add with two arguments a and b like this:
> add a b = a+b
Or this way
> add’ a b = (+) a b
Then we apply the function to the two arguments, let’s say 5 and 9:
> add 5 9
=> 14
We have just defined a function with two arguments. Now we can use the Haskell interpreter and feed the addends to the function, or in other words apply the function to its arguments. Could this be any easier or simpler Pate?”, says Selma.
”Well, it can’t”, replies Pate. ”This is as clear as it can be. Now our add function can be fed with any two arguments we want, and we no longer need to use the predefined ones such as firstNumber or secondNumber, but we can define our arguments on the spot. This makes out machines truly reusable.
Now anyone can take the add function and use it with their programs and they would not need to know anything about firstNumber and secondNumber. Just like us, they could use the Haskell interpreter and give their own arguments to the add function. We might also get the arguments from the outside our program. These computing machines are deterministic, but we have free will. At least what comes to us dogs defining our own arguments”, says Pate.
”There is always room for good add and double functions”, says Pate. “I remember a day when I had behaved really well, obeyed all the instruction that I was given and had not barked once. My master promised to give me a double serving of chicken jerky treats because I had behaved well. Had I had the double function defined on my Haskell interpreter, I could have been able to calculate how many yummy chicken jerky treats to expect. But when it comes to programming it’s never too late for an old dog to learn new tricks! I can now demand what I deserve, and I can even change my double function to become a triple function, just like that.
> tripleMachine = (*3)
These functions are extremely useful. There is nothing more important than to be able know exactly how many chicken jerky treats there is to come. So easy and so practical and with so little coding. Not bad, eh? We need more such machines with chrome plated pipes!”, says Pate and adds “I mean more functions with big enough numbers as arguments”.
”But there is one more thing I am uncertain about Selma. What if our masters accidentally give a function an argument of wrong type, such as giving a character ‘a’ to a function that should be fed with a number? Hopefully the function is not evaluated in a way that would end up us not be given any chicken jerky treats at all”, says Pate.
“No problems Pate. The Haskell interpreter is so smart that it stops that from happening. A function can’t be fed with an argument of a type that the function can’t handle. Give it a go and try. Try to give an argument of type character, such as ‘a’ to our double function and see what happens.”
> double ’a’
=> * Couldn’t match expected type `Int’ with actual type `Char’
”There you go Pate. As you see it does not work. We just tried to transport some sand in a pipe that can only transport water, and that’s why we get the error. It is expecting an integer and we are feeding it with a character. That is not a good idea. It sounds a bit mad to double an ‘a’, doesn’t it? Smart Irish wheaten terriers never try to put sand into a water pipe or water into a sand pipe.
So, our functions are smart. They can never be fed with arguments of wrong type. It would be great if real water pipes were also designed that way. If there were always two separate pipes, we would never risk dirty water going into a freshwater pipe because of a valve left open at a T-junction of two pipes. We are pipe safe and type safe!
Also, our functions can infer all sorts of things. Functions won’t let arguments of wrong type in, but simply stops this from happening before we even get to use the functions on anything – before we even get to start our program. Dogs love functions that function. We tend to do a lot of mistakes, and it would be catastrophe if we couldn’t get our chicken jerky treats in right numbers.
This is absolutely the best way to write programs for dogs. We can simply define all sorts of fancy functions, and the functions are always fed with just the right arguments always, no exceptions. The functions get the stuff they can deal with. That’s what I would call a doggishly smart programming language. How does that sound for a way to write programs Pate?”
“It sounds the way I like”, replies Pate.
“I am glad to hear that! We can now move on to building programs that can make decisions. This has been quite a load for our doggish brains and we sure need a reward, too. Let’s reward ourselves with chunky chicken jerky treats, one each”, says Selma.
”Machines are for puppies, we go for the functions and we certainly need our yummy rewards!”, says Pate.
Comparing numbers
”it is fun to add numbers to together, but there is one important piece missing from this thing”, says Pate. “How could we compare those numbers? How could I compare the number of chicken jerky treats I have had last week to the number of chicken jerky treats I have had this week? Just for watching my weight, it would be good to be aware those numbers. We Irish wheaten terriers should take care of our health to avoid the extra pounds. But that being said, a chicken jerky treat every now and then is reasonable. Could you explain how this comparison problem could be solved?”
”I sure can Pate. Numbers can be compared by comparison functions. A number comparison function is fed with two numbers as arguments and the function will evaluate to either True or False. Comparison functions come in many shapes and sizes. Let’s get introduced to two of them.
Comparison functions reflect how things relate. There are many such functions, but maybe one of the best known is the one that can tell us if two numbers are the same or not. It is the equal to function.
The function is named == and it is used the same way as the add function. Even the arguments are of the same type as for the add function. The arguments are of the same type, but the value of the function is of different type to the add function. == function’s value is either False or True. The value depends on the arguments of course. == function evaluates to True if the value of the argument on the left is equal to the value of the argument on the right.
Notice that == function can be used just like any other comparison function. The arguments of the function can be written after the function name or around the function name. Let’s look at the example:
> (==) 1 1 — arguments after the function name
=> True
> (==) 1 2 — arguments after the function name
=> False
> 1==1 — arguments around the function name!
=> True
> 1==2 — arguments around the function name!
=> False
”Ok. That’s nice, but I would also like to see a function that could tell me if I got this week more treats than the last week. What would that kind of function look like?“
”I got so excited about the == function that I forgot your original need for comparison functions. In order to know, if we had more treats this week than the last week, we need a > function. This is how we do it. We simply change the name of the machine from == to > and feed the arguments to the function as always.
> (>) 2 1
=> True
> (>) 1 2
=> False
”Eeeh! I should have guessed that. It is as easy as to simply change the name of the function. I guess the function is called greater than. And I am pretty sure < function is the opposite of greater than”, says Pate.
”Yes it does. Remember Pate that there are many other comparison functions for numbers, too. There are two well-known comparison functions, in addition to the ones we just saw. One is the /= function and another one you already guessed, namely the < function. /= is the not equal to function and < function is the less than function.
< function evaluates to True if the value of the argument on the left is less than the value of the argument on the right, otherwise the function evaluates to False.
/= function evaluates to True if the value of the argument on the left is not equal to the value of the argument on the right, otherwise the function evaluates to False.
Now, I guess this is enough of comparisons for now. Let’s move on to the exciting world of characters as strings. New types coming up!”, says Selma.
Chapter 5. Characters and strings as arguments
Integers are great but now we get to know two new types which are character and string. Or to be exact, we only get to know one new type character because string is just a list of characters and list is something we know already.
Integers fit many functions, but what kind of functions could be applied to things like ‘a’ and ‘6’. ‘6’ looks like a number but it is a character and cannot be fed to add or double function. Characters are defined by using single quotes around the character. Character is an important type in many programming languages. A list of characters is called a string. Remember that a character such as ‘t’ can be thought as being created by a function that evaluates to character t. We can think that each character is picked up from a set of characters. This could be defined like this.
data Char = ’a’|’b’|’c’|’d’…
This simply means that we can pick one out of a set of many. If you still remember how we defined our first simple function with integral numbers. Integral numbers is also a set, a set of integral numbers. We just pick one and there we have an integer.
data Integer = … -2 | -1 | 0 | 1 | 2 …
The Char and Integer definitions above are not proper Haskell, but they will give us some intuition on that everything needs to be constructed and we get nothing out of thin air. We can think of ’a’ as a special type of function, a value constructor, because it constructs a character value. The same way we can think of -1 as something that constructs us a value of negative number 1. It may sound funny, but – (minus sign) is also a function that operates on one argument by negating the argument. If – function is fed with two arguments, such as a-b, it behaves like a classic subtract function where b is subtracted from a.
But let’s introduce ourselves to functions that can be fed with characters. One such example is a function that transforms lower case letters to upper case letters or the other way round. Look at the function Pate. It transforms any character to a lowercase character. This is what toLower function looks like.”
> toLower ’S’
=> ’s’
toUpper function in turn transforms a character to an uppercase character
> toUpper ’s’
=> ’S’
Comparing characters
”Did you know that there are many functions that are fed characters as their arguments. Just like with numbers there is a function to compare if two characters are the same. The function is named the same way as the function that compares the equality of numbers, namely ==. Also, the function is used the same way as with the numbers but the arguments are of different type. Both functions evaluate to the same type of values True and False.
== function when used with characters, evaluates to True if the value of the argument on the left is equal to the value of the argument on the right, otherwise the function evaluates to False. The result of the evaluation depends on the arguments that are fed to the function. Let’s look at an example:
> (==) ’a’ ’a’
=> True
> (==) ’a’ ’b’
=> False
”There is one thing I am wondering about”, says Pate. “When we compare the characters, we use wording such as equal. But equality refers to mathematics. Can we also say that one character is greater than another? Or could one character be less than another character? Even if we have a character such as ’A’, we do not say that it is greater than ’a’. At least the meaning is not the same as saying that 5 is greater than 2. What is this all about? I do not quite get this equality comparison stuff. Could you explain it in a bit more detail Selma?”, continues Pate. Would it just be enough of the letters to say that they are either equal or not, but that no letter is less than another letter?
”I sure can!” says Selma. ”It is truly fun to ponder what it actually means to say that two things are equal or the same. It is a question of definition. You could put your friends in the order of preference. Is Topi preferenced to Selma, or are they equally good? When you want to know which of the friends is better than another you need to define friend comparison functions. The functions reflect how the arguments relate.
Those functions could tell the preference between your friends. That sounds like true artificial intelligence, does it?”, says Selma winking her eye. ”You simply need to define a function that can tell the preference. Putting friends in the order of preference is something that it might be a good idea to hide the function from everyone else except for the best friend. Everyone wants to be the best friend of someone, but no one wants to be at the end of the preference list. Who would not want to know that he is someone’s best friend?
If there is a sequence of numbers such as {1,2,3,4…}, the numbers towards the end of the list are said to be greater than the numbers at the beginning of the list. 4 is greater than 1 because it is listed after 1. The same goes for a sequence of characters such as {’a’,’b’,…’z’} as we have already seen, when we discussed value constructors. If a set of numbers is defined by value constructors, the latter value is considered greater than the former. It is a question of defining the order. If the alphabets were defined as a set of {’z’,…’b’,’a’}, ‘a’ would be greater than ‘z’.
Now, when we compare characters such as ‘a’ and ‘z’. ‘z’ is greater because it happens to be after ‘a’ by definition. If two characters are at the same place in a sequence of characters, they are considered equal. Just like if two numbers are at the same place in a sequence of numbers, they are considered equal. Let’s look at some code.
> ’a’>’z’
=> False
> ’a'<’z’
=> True
With this information we can get started and build all sorts of functions. Because us dogs can’t recall long passwords, we can build a password comparison function that is fed with a single character only. The function could compare two characters and it would evaluate to True if the characters were the same and it would evaluate to False if the characters were different.
We could name the function to reflect its job. Because we only compare characters, let’s name it passcharactercomparison. How does that sound for a function Pate? Is it doggish enough a name?”, asks Selma.
”Sounds perfect Selma!” continues Pate. “Now let’s write the function!”
> passcharactercomparison = (==)’p’
> passcharactercomparison ’t’
=> False
> passcharactercomparison ’p’
=> True
”It works!”, says Pate. ”If I feed the function with argument ‘t’, the function will compare it to ‘p’ and the function evaluates to False.
If I feed the function with argument ‘p’, the function will compare it to ‘p’ and the function evaluates to True. This is really smart thing”, says Pate.
”It sure is”, says Selma. “Because the passcharactecomparison function has already been fed with one argument (‘p’), it expects to be fed with another one before the function can be evaluated. It needs another character to be able to compare something to ‘p’. Once it is fed with another character, the value is evaluated to True or False and we get to know if our passcharacter is right or wrong.
Strings as arguments
”A list made of characters is called a string. As we have seen at the beginning of the book, double quotes around a word can be thought as a function that evaluates to a list of characters. Can you think of some use for strings?”, asks Selma.
”I could figure something out”, replies Pate and keeps thinking. ”Even though a paw print is every dog’s signature, it would be great if we could print our initials to to a marrowbone. Then all dogs would know whose bone it was, and there would be no quarrels about it.”, says Pate. ”But how would we define such a function then?” asks Pate.
”If a function were fed with two strings, first name and surname, it could pick the first letter of the first name and the first letter of the surname, and produce those letters separated by a dot. Because strings are lists of characters, our function should be able to pick one character at the beginning of each string and then combine them into one string. It would be great to see such initials printed on the side of a tasty marrowbone.
Now, we should find a function that could produce the first item of a list. Such function is called head. Can you still recall the function we used to produce a list Pate?”
”Yes I do. We listed the items in the brackets and ended up with a list of items”, replies Pate like a pro. ”We could use head functions of which the first one would be fed with first name and the second one would be fed with surname. Then we could simply put these functions in brackets and separate them by commas. There we have it, a string with initials. That’s what we are after, right? But what would the code look like then?”
”It would look like this”, replies Selma.
> initials f s = [head f,head s]
> initials ”Selma” ”Erkkilä”
=> ”SE”
”But hey! Shouldn’t we add a dot between the initials?” asks Pate observant.
”Oh, yes! Good point Pate! We need to write our program according to the specification and the dot between the initials is certainly part of that specification”, says Selma. ”But, no worries, let’s fix it. We could write the code this way.”
> initials’ f s = [head f,’.’,head s]
> initials’ ”Pate” ”Ilonen”
=> ”P.I”
”If we made a word processing program, there would very likely be a requirement to combine two words. Then we might need a function that could produce one string out of two.
Such a function is named ++ and called concatenation function. ++ function is fed with two strings and it produces a third one. We can try out the function like this.”
> (++) ”firstpart” ”secondpart”
=> ”firstpartsecondpart”
or this way
> ”firstpart”++”secondpart”
=> ”firstpartsecondpart”
The combining of two strings is called concatenation. We simply concatenate two strings (lists) and end up with a new string (list). When we know how to deal with integers, characters, strings and lists, we can define all sorts of functions with our dog friends. Pate, now that you know how to define initials function, you can teach the trick to your friends Topi and Orvokki, too.
”I sure will teach Topi and Orvokki how to define the initials function once we see at the dog park. No more arguments about bones. Digitalization, here we come! Functional programming can be applied to many problems. I wonder if our masters know how many applications there are to these things?”, says Pate.
Comparing strings
”By the way Selma, it would be nice to be able to compare strings, too. Are there functions that could do that for us?”
”There sure are and many”, says Selma. “If you feed a function with a password that has many characters, we need to figure out if the password is right or wrong. In order to do that, we need to compare the string that was fed to the function against the string that was fed to the when the function was first defined. It could look like this.
Lets define the passwordcomparison function like this
> passwordcomparison = (==)”chicken jerky treat”
Lets feed passwordcomparison function with ”pellets”.
> passwordcomparison ”pellets”
=> False
Lets feed passwordcomparison function with ”chicken jerky treat”.
> passwordcomparison ”chicken jerky treat”
=> True
”We can use == function to find out if two strings are equal, just like we did with numbers and characters.
Because the passwordcomparison function has only been fed with one argument, it is expecting another argument before it gets evaluated. Once the second argument is fed to the function, it finally evaluates to True or False. Then we can tell if the strings are equal or not.”, sums up Selma.
More intelligence
”Good morning Selma! How about learning more programming? What’s on the menu today?”
”Hi, Pate! Today we could make our programs and functions a bit smarter. How is that for a plan?”, replies Selma.
”Agreed! Us dogs are never too smart to write even smarter programs. Let’s start!”
”So be it”, continues Selma. “We know that functions often evaluate to different values, if they are fed with different arguments. Let me introduce you the evaluateFood function. The function can produce an evaluation of the food that it is fed with. Let’s look at the code.”
evaluateFood food
|food == ”chicken jerky treat” = ”Excellent and tasty”
|food == ”minced meat” = ”Quite tasty”
|food == ”pellets” = ”Not that tasty, but healthy”
”Just a moment. I can see new symbols and all sorts of things”, says Pate. “I know the == function. It is the function to check if two things are equal. Also I can recognize the equal sign that has things on its left and things on its right. But what on earth is that vertical slash? Are we back to using these tally marks or what is this all about?”
”You have been reading this book carefully!” says Selma. “That vertical slash is called a guard. If we use guards, we can inspect values and decide which function should be evaluated next. If the == function evaluates to True, we will pick the function on the right side of the equal sign. If the function is fed with ”chicken jerky treat”, the == function evaluates to True and the function on the right side of the equal sign is evaluated and the value will be ”Excellent and tasty”. Give it a go Pate.”
> evaluateFood ”chicken jerky treat”
=> ”Excellent and tasty”
> evaluateFood ”minced meat”
=> ”Quite tasty”
”If we use guards, we can branch in our program. Let’s see another example.”
treatsInAWeek x
|x<1 = ”You have not had any treats!”
|x>=1 && x < 4 = ”You have had some treats!”
|x>=4 = ”You have had far too much treats!”
> treatsInAWeek 4
=> ”You have had far too much treats!”
> treatsInAWeek 0
=> ”You have not had any treats!”
”That is quite a program!” says Pate. ”By the way, what are the two & symbols there? I have never seen anything like that.”
”What a good question!”, says Selma. ”As you can see, there are comparison functions on the left and right of &&. && function performs logical and operation. Whenever both functions, one on the left and another on the right, evaluate to True, the && function evaluates to True, otherwise && evaluates to False. So, && is a function that needs two arguments. True and False can also be called truth values.
|| function performs logical or operation. || function evaluates to True if at least one of the comparison functions on its left and right evaluates to True.
Everything looks more familiar when we represent the functions like we did at the beginning of the book. First comes the function name and then the arguments – two other comparison functions. So, first && function and then the arguments. Look here.”
|(&&) (x>=1) (x<4) = ”You have had some treats!”
”Now it should be crystal clear that && function is fed with two comparison functions as arguments. There is an unusual number of parenthesis here, but we should not be too worried about them for now. You can still figure out the logic of how everything works. && function evaluates to True or False depending on the values of the other two comparison functions.
If we think about the time of evaluation, we can think that there is a sequence of three functions of which the first is fed with the evaluation results of the functions that follow. Easy, eh?
By the way, a guard is also a function. If | evaluates to True, the function to the right of the equal sign will be evaluated. The point is that there could be many guards. If we have three guards, our code can branch to three different directions.
Think about it. When each guard on the evaluateFood function is evaluated, the corresponding function on the right side of the equal sign will be evaluated. Functions that evaluate to truth values are called predicates. Guards are needed for branching and they need to be fed with a predicate function. If the predicate evaluates to True, the function on the right side of the equal sign will be evaluated.
But what if there is no match? What is we accidentally feed evaluateFood function with something like “chocolate drop” and there is no match? To make sure our function always evaluates to something, we need to add one more line of code and specify what will happen if none of the guard conditions match. For that we use otherwise that evaluates to True. This is how we do it.”
evaluateFood food
|food == ”chicken jerky treat” = ”Excellent and tasty”
|food == ”minced meat” = ”Quite tasty”
|food == ”pellets” = ”Not that tasty, but healthy”
|otherwise = ”Do not know that food at all”
If you use && function, || function and guards, you can add as much intelligence to your program as you like.”
Chapter 6. Pattern matching and chicken jerky treats
“By the way Pate. Do you know how much dog food costs these days?” asks Selma.
”No idea, because I never need to pay them myself”, replies Pate.
”I happen to know. I made a program that can tell me how much each food costs. It’s like a programmatic price list. Let me show you how to do it. It is a piece of cake”, says Selma.
price ”chicken jerky treat” = 70
price ”minced meat” = 38
price ”pellets” = 22
”Is that really all there is to the function that can tell us how much each food costs? How does it work?” asks Pate.
”Well, the price list function needs to be doggishly easy. We simply define the prices for each food item. The usage is really simple We simply feed the price function with the name of the food.”
> price ”chicken jerky treat”
=> 70
> price ”minced meat”
=> 38
> price ”pellets”
=> 22
”It really works”, says pate. “It looks really simple, but does it work? How can there be three functions with the same name, price.
”Listen Pate! Actually there is only one function named price and we have three alternatives of the same function. Our price function can now recognize three different values, namely ”chicken jerky treat”, ”minced meat” and ”pellets”. Let’s write the code again and use the case expression. Then we can see that there is only one function.”
price food = case food of
”chicken jerky treat” -> 70
”minced meat” -> 38
”pellets” -> 25
”As you see Pate, we only have one function named price”, says Selma. “Function is fed with the food’s name. Our function is smart. It can recognize the argument it is fed with and pick the right price accordingly.
“When an argument is fed to the function, the argument will be matched against the patterns listed.
First we check if the argument matches with the pattern ”chicken jerky treat”. If it does, we evaluate what’s on the right side of the arrow.
If it doesn’t, we check if the argument matches with the pattern ”minced meat”. If it does, we evaluate what’s on the right side of the arrow.
If it doesn’t, we check if the argument matches with the pattern ”pellets”. If it does, we evaluate what’s on the right side of the arrow.
If it doesn’t, we end up in an error message and our program fails.
By the way, Pate. Could you write a function that could tell the name of a food by its price. I will show you!”
food price = case price of
70 -> ”chicken jerky treat”
38 -> ”minced meat”
25 -> ”pellets”
=> food 70
=> ”chicken jerky treat”
”It is important to notice that we did not compare the prices or foods to other prices or foods by using a comparison function such as ==. Instead we relied on pattern matching to recognize the argument.
”What?”, says Pate. ”Isn’t pattern matching when we try to recognize images? Such that if there is a dog in the picture, a program could tell that it really is a dog. In case there is a person who does not know what a dog looks like?”
”That is called image recognition, but the idea is the same as with pattern matching.”, replies Selma. ”In this context pattern matching is a perfect way to do the kind of things we just did. If an argument matches with the pattern, we choose to evaluate what is on the right side of the equal sign or in case of a case expression, we evaluate what is on the right side of the arrow.
But there is much more to pattern matching than really meets the eye. Later I will show you how we can tell if bag of chicken jerky treats contains one jerky, many jerkies or no jerkies by matching patterns. Before we do that, we need to familiarise ourselves with lists more carefully, though.”
Chapter 5. From chicken jerky bags to lists
Lists and list related functions
”A List is probably the most important tool of any programmer”, says Selma. “This is because there is plenty of fine functions that we can apply to lists. Dealing with lists is not only fun but also easy. With lists it is easy to organize not only bags of chicken jerky treats but also many other things. Let’s start by creating a list that represents an empty bag of chicken jerky treats.
> list0 = []
When we want to add a couple of treats, we need a function that knows how to do it. Let’s add the treats to the list one by one by using : function. : is a function that can add a new item to the beginning of any list and create a new list. The new list contains the new item followed by the items of the old list.
> list1 = ”treat1”:list0
> list2 = ”treat2”:list1
> list2
=> [”treat2″,”treat1”]
Now we can see that there are 2 treats on the list. We can add new items to the end of the list with ++ function. This is how we do it.
> list3 = list2 ++ ”treat3”
> list3
=> [”treat2″,”treat1″,”treat3”]
What if we want to know how many treats there are on the list?” asks Selma.
”Oh.. mmm”, says Pate. ”I wonder if there is a function such as please_calculatthe_number_of_treats_in_the_bag, because no matter what, the solution is always a function.”
”There sure is”, replies Selma. ”You have certainly understood the point. The solution is always a function, we just need to find out what kind of a function. Have a look at the picture of a length function. The function is fed with a list of treats and the function will calculate the number of treats on the list.”
Picture 3. A function that calculates the number of chicken jerky treats on a list.
> length treatlist
=> 2
”Length is a handy function. It is fed with a list and it knows how to calculate the number of items on the list. Now it is very easy to keep track of the number of treats, and make sure that no dog has been sneaking into your precious chicken jerky treat bag.
In addition to length, there are many other functions which take lists as their arguments. Other important functions that operate on lists are head and tail.
With !! function we can produce an item of the list. !! function is fed with an argument of type integer. Feeding 0 to the function means that the function will produce the first item of the list, feeding 1 means the second item of the list and so on. Notice that the arguments of the !! function are typically fed around the function name. First comes the name of the list, then comes the function name !! and last comes the integer.
> [”treat1″,”treat2″,”treat3”]!!0
=> ”treat1”
> [”treat1″,”treat2″,”treat3”]!!1
=> ”treat2”
With the head function we can produce the first item of the list.
> head [”treat1″,”treat2″,”treat3”]
=> ”treat1”
With the tail function we can produce the list without the first item.
> tail [”treat1″,”treat2″,”treat3”]
=> [”treat2″,”treat3”]
Notice that head produces an item and tail produces a list.
> head [”treat1″,”treat2″,”treat3”]
”This is awesome!”, says Pate. “Now I will give you such a puzzle that if you can solve , I am sure to give you an extra tasty treat from my bag. Let’s assume that we have a bag of many kinds of treats, not only chicken jerky treats. How could we calculate the number of each type of treat in the bag? Is it possible to write such a program?
“That is a tough one”, replies Selma. “But I think it is just a question of finding the right functions for the job. I think we can solve the problem with the filter function, which is introduced in the next chapter. Now I will tell you a couple of things about lists and pattern matching as I promised.”
Lists and pattern matching
”As I promised, I will now tell you how to explore lists with pattern matching. Look at this example.
selmasShoppingList = [”Chicken Jerky Treats”, ”Pellets”, ”Minced meat”,”Dog chocolate”]
checkShoppingList [] = ”The shopping list is empty”
checkShoppingList [x] = ”There is 1 item on the shopping list”
checkShoppingList (x:xs) = ”There is more than 1 item on the shopping list”
”As you see, selmasShoppingList has 4 items. If the checkShoppingList function is fed with an empty list, it can produce the string ”The shopping list is empty” to communicate that the list is empty. The pattern of an empty list is [].
If the checkShoppingList function is fed with a list with one item, the function will produce ”There is 1 item on the shopping list”. The pattern of a one item list is [x]. The x can be replaced by any name.
If the list has more than 1 item, the function will produce ”There is more than 1 item on the shopping list”. The pattern for more than 1 item in this case is (x:xs). The x is the name for the first item of the list and xs is the name for the tail of the list. Notice that because xs could also be an empty list, (x:xs) also matches with a one item list – it matches with any list with at least one item. Another way to represent a pattern for one item list is (x:[]).
You can try to apply the function to an empty list, to a list with one item and to a list with many items. Then you can see how it works. In this case we could replace the last pattern (x:xs) with _ which means any value. Then our program would look like this.
selmasShoppingList = [”Chicken Jerky Treats”, ”Pellets”, ”Minced meat”,”Dog chocolate”]
checkShoppingList [] = ”The shopping list is empty”
checkShoppingList [x] = ”There is 1 item on the shopping list”
checkShoppingList _ = ”There is more than 1 item on the shopping list”
”That is really handy!” says Pate. “When we use pattern matching, we can see the kind of arguments we are expecting to be fed to the function, and we can produce something accordingly. If there were a whole lot of things on the shopping list, we would take a big shopping bag with us. If the shopping list was empty, we would not need a shopping bag at all, and we would not even need to go for shopping. If there was just one item on the shopping list, we would only need a small shopping bag. Could it happen that we went for shopping and bought something spontaneously? People tend to act that way, but what about us dogs? Could it happen to us, too?”
“That is a very interesting question”, replies Selma. “Our doglike examples do not have any spontaneity in them. Spontaneity could be represented by randomness in our program. Randomness is an interesting thing, but for now we do not need to worry about it. I promise to introduce you to randomness later, and we get to act like our masters sometimes do, when they shop impulsively and base their decisions on guessing.”
”All right! At this stage we deal with function whose arguments define the outcome of a function. Maybe it is better that we do not deal with functions that can have unpredictable results. It is a scary thought. It is much nicer to always get the chicken jerky treat, if you sit or roll rather than get a treat every now and then. Being praised is awesome, but as a reward chicken jerky treat unbeatable. Certainty is nice, certainly”, says Pate.
”There is one more thing about pattern matching I would like you to pay attention to. Remember that the matching order makes a difference. If there are several patterns one after another and you make the first pattern _ ,which means “any pattern”, you would always end up with “There is more than 1 item on the shopping list”. This is because “any pattern” matches with any argument and therefore it does not make sense to have it matched first! Did I get my point across?”, says Selma.
”I see. That is a very important thing to remember. Would the same apply if we were comparing values with comparison functions instead of using pattern matching?” asks Pate.
”Yes, indeed”, replies Selma. ”The same applies to if we are comparing values. We need to match the argument against the most common patterns first and leave the least common patterns in the end of the sequence”, says Selma.
”A-ha”, says Pate. ”This is a good rule for exploring any set of possible arguments. It also applies to any dog’s life. Do the most important things first and leave the rest for later time. And the things that tend to happen often, should be checked first. That will speed up the execution of the program!”
Chapter 6. Filter function
”Let’s define a list with four tasty foods of which two are the same.
treatList = [”Chicken jerky treat”,”Chicken jerky treat ”,”Dog chocolate drop”, ”Marrowbone”]
“Now we have a task. We should pick chicken jerky treats from the list and count their number. Then we should pick dog chocolate drop from the list and count their number. Finally, we should pick the marrowbone from the list and count their numbers. If you had to define a function that could choose items from a list, how would you do it?” asks Selma.
”Well… At first, all the items were mixed up in a big bag. Then I would choose the best treats and place them in one of the empty bags. The I would pick the dog chocolate drops and place them in another empty bag. Finally, I would pick the marrowbones and place them yet in another empty bag. Then I would add a sticker to each of the bags to that would say what’s in the bag.
”We could now write a program where each bag would be presented by a list, and then we could apply the length function to each list. Then we would know the number of items in each bag, right? The length function knows how to count the items on each list, isn’t it so?” asks Pate.
”You’re right!” replies Selma. ”We just need to find out, how the choosing function could work. Can you figure it out Pate?”
“At least, I could give it a go”, says Pate. “Somehow we need to tell the choosing function what we want to choose. We need to give the function some kind rule on how to pick the items from the bag such as ”pick all chicken jerky treats from the bag and place them in an empty bag”, and then add a sticker saying “chicken jerky treats” on the new bag. What do you think Selma?”
”That’s exactly how we need to think Pate. You are such a clever dog. Let’s see the kind of functions we can define from these ideas”, says Selma.
Picture 4. A function that picks chicken jerky treat items from a list.
chickenJerkyTreatList = filter(==”Chicken jerky treat”) foodList
”Look at the picture above Pate”, continues Selma. “Filter function is such that it applies a comparison function to each item on the list. Whenever the comparison function ==”kanaherkku” evaluates to true, the corresponding item is created on the new resulting list. So, the filter function is fed with two arguments: a comparison function and the list to be filtered. Notice that the filter function’s argument is also a function. Filter function is called a higher-order function because it is fed with another function.
The picture 5 depicts how we pick all items from the list that contain “Dog chocolate drop”. The filter function is used to create a new list that contains only “Dog chocolate drop” items. The same idea is applied to ”Marrowbone” items in picture 6.
Picture 5. A function that picks dog chocolate drop items from a list.
dogChocolateDropList = filter(==”Dog chocolate drop”) foodList
Picture 6. A function that picks marrowbone items from a list.
marrowBoneList = filter(==”Marrowbone”) foodList
”Now that foods are listed on their respective lists Pate, it is easy to count the number of each type of food. We can simply apply the length function on each list.”
> chickeJerkyTreatCount = length chickenJerkyTreatList
> marrowBoneCount = length marrowBoneList
> dogChocolateDropCount = length dogChocolateDropList
Combining two functions
”That was easy”, says Pate. “By the way, do we always need to do this thing in two steps. First we define the chickenJerkyTreatList, and then chickenJerkyTreatCount. Could we end up with the right counts of each type of food without such intermediate steps?” asks Pate.
“We sure could!” replies Selma. “As a smart dog you can combine the chicken jerky treat choosing function (filter) with the counting function (length) as if there was only one function. This combined function is fed with a big bag of foods that contains all sorts of treats, drops and bones and the comparison function such as ==”Chicken jerky treat”. The output of the combined function is the number of the chicken jerky treats in the big bag. The next picture depicts the function that can calculate the number of chicken jerky treats in the bag.”
Picture 7. A function that produces a list containing chicken jerky treats combined with a function that counts the items of the produced list..
chickenJerkyTreactCount= length(filter(==”Chicken jerky treat”)treatList)
”We can think our program as a reduction or simplifying task. First, we apply the filter function to the treatList like this filter(==”Chicken jerky treat”)treatList which evaluates to [”Chicken jerky treat”,”Chicken jerky treat”]. Secondly, the output of the filter function is fed to the length function. The length function is applied to the output of the filter function. We pick all items that contain ”Chicken jerky treat” from the treatList and count their number.
Let’s look at this in more detail. To start with we create a new list that only contain ”Chicken jerky treat” items. The new list is achieved by first applying the argument of the filter function ==”Chicken jerky treat” to each item of the treatList. When the list full of ”Chicken jerky treat” has been created we apply the length function to it which produces the number of ”Chicken jerky treat” on the treatList. Not a bad way to write the program Pate?”
”Not at all”, replies Pate. “If I understood you correctly, the whole program is a big reduction task where parenthesis get removed one after another – but could it really be so simple?”
”Yes it can Pate. Simple is beautiful!” says Selma. “Here are the functions for figuring out the numbers of marrowbones and dog chocolate drops, too. If you want good practice, you can draw similar diagrams of those functions, too.”
marrowBoneCount = length(filter(==”Marrowbone”)herkkuLista)
dogChocolateDropCount = length(filter(==”Dog chocolcate drop”) treatList)
”Listen to this Selma”, says Pate. ”In order not to repeat the function such as ==”Marrowbone” everywhere in the program, could we fix the issue by giving the comparison function an argument instead of having fixed values such as ==”Marrowbone” to make the program more reusable?”
”Yes indeed Pate. We could define a new function isMarrowbone. The name starting with “is” sounds good since == function always returns True or False. It makes sense to “ask” if the treat is a ”Marrowbone” or not. We can think that True means yes and False means no answer. It resembles a natural language. We can write our function this way.
isMarrowBone = (==”MarrowBone”)
If we want to use pattern matching, we can so it this way.
isMarrowBone ”Marrowbone” = True
isMarrowBone _ = False
Then we simply change our code like this
marrowBoneCount = length(filter(isMarrowbone)treatList)
Now we can use isMarrowbone function whenever we need to check if a string is ”Marrowbone”. By doing this we no longer need to write ==”Marrowbone”, but can write isMarrowbone instead. This is more readable than using ==”Marrowbone”. Also, if we misspelled marrowbone and our function would be ==”arrowbone”, we would no longer be counting marrowbones but arrowbones. If we use the same function everywhere in our program, it is easier to get everything right in the first place.
”The program seems to work, but I still wonder if the code is as smart as it could be”, asks Pate. “I see a great deal of repetition in the code. Repetitio mater studiorum est, but could we get rid of those similar looking lines of code. In writing software there is a saying do not repeat yourself or DRY. Should we follow the DRY principle and try to make the solution a bit more compact? For example, the functions such as marrowBoneCount and dogChocolateDropCount that count the numbers of different treats only differ by the arguments fed to the filter function. In the end we seem to be to be producing a distribution of treats in the big bag.
Now that the names of the treats are listed in the treatList, could we simply use the names of the list as they are? Now we use the names “manually” by writing each of them when we deal with the comparison functions. We needed a list that would contain unique items of the treatList, a list where every item would be different.
Then we would know the set of unique items. Coming up with a distribution of treats in the bag with 50 different treats would be a tough task to deal with manually, eh? I can easily imagine 50 different chicken jerky treat brands. We would be seeing a lot of functions ending with Count and List along with a lot of spelling mistakes with treat names, if had 50 different treats in the treatList. Simply put, our program would be a big mess. There must be a better way!”, says Pate.
”You are dead right Pate, again”, replies Selma. “We can make out program much smarter. And we sure can reuse the names on the treatList. It makes no sense to write the names again and again, but to extract the unique treat names from the big bag of treats. How would we write such a program?”
”That is a tough call Selma, but let me give it a go. If we came up with a set of treats (unique items), we could use the set to find out the number of each treat on the treatList. So, we need two lists. One that contains all the treats and another one that contains the unique items only. Finally, having these two lists we could produce a third list whose items represent the count of each treat – our treat distribution.
We would first take the first item of the treat set and feed the item to a function that could use the item of the set as its argument and count how many times the item appears on treatList. We could repeat this for all items on the set.
”Sound reasonable”, replies Selma. ”But how on earth are we able to get a list of unique treats from the treatList? Maybe use a function?”
”Function indeed!”, replies Selma. ”Such a function has already been invented and it is named nub. Nub function is fed with a list and it will produce a list with unique items – a set. How about using that kind of function?”
”Wow!” replies Pate. ”That is exactly what we need. Now that we know how to produce a list of unique items, how do we use it to solve the problem? How do we get those original strings replaced by the strings that are present on the unique set produced by the nub function?”
”Listen Pate!” replies Selma. ”We can get things sorted out by introducing a new function. It is the map function. Map function is fed with a function and a list. As it is fed with a function, it is a higher order function just like the filter function. Map function will apply a function to each item on the list and that’s exactly what we need for now. Map function is one of the most important functions in programming and it ought to be learnt well. Your friend Topi will be green with envy, if you tell him that you know how to use the map function. You could teach Topi how to use the map function, too.
Chapter 7. Map function
”Listen to me Pate! Now it is time to get to know the map function. It is a delicate function which is used in a number of programming languages of today.“
“That sounds interesting!” replies Pate. “What is so special about the map function then?”
”Have you heard about a kennel where each dog had their daily number of treats raised by 3?”
”I have not”, replies Pate. “It would be nice to live in such a kennel where the number of treats could be incremented for all in a blink of an eye. But we must remember that treats should make up no more than about 10% of our daily calories. That would be a kennel to my taste.”
”Sure would”, replies Selma.”Let’s imagine that we have a kennel of 5 dogs: Selma, Topi, Repa, Motti and Pate. The current number of treats per day were the following.”
Selma, 2
Topi, 3
Repa, 5
Motti, 1
Pate, 3.
”The daily number of treats for each dog could also be represented by a list [2,3,5,1,3].
If the daily number of treats were added 2, the new treat numbers would be [4,5,7,3,5]. Each dog’s daily number would be added 2. It is hard work to manually add number 2 to every dog’s daily treat number. What if we have a kennel of 200 dogs? There is plenty of work to be done while each dogs’ treat number needs to be transformed one by one.
Wouldn’t it be nice if we could deal with lists just like we can deal with single values? If we can raise Topi’s daily treat number by 2, we could ask a question whether we could do the same thing for all the dogs in one go? If we did the job manually, we would soon be running out of paws and pencils.
And the next question would of course be if there were a function that could do the job for us. Such a function would be fed with another function that would know the kind of transformation we want to apply on each treat number and a list of dogs’ current treat numbers. So, two arguments would be needed, a function and a list.”
”That sounds smart”, replies Pate. ”I am eager to see how we apply the map function to this problem and to the list of treat numbers. Can we see the code?”
”Sure”, replies Selma. ”This is how it works. Have a look at the diagram and the program.”
Picture 8. The map function is applied to a list of treat numbers and each item on the list is added 2.
> treatNumberList = [2,3,5,1,3]
> newTreatNumberList = map (+2) treatNumberList
> newTreatNumberList
=> [4,5,7,3,5]
”That sounds really advanced”, says Pate. “+2 seems to be the rule by which the number of treats is to be transformed. Every dog’s treat number is added 2. By using the same rule, we could as well subtract 2 from the current treat number. If all the dogs of the kennel decided to chase a rabbit without a permission, they might face a notable decrease in the daily treat numbers. We need to be careful! Map function is a two-way street, eh?” asks Pate and smiles.
”It sure is, and actually it is more than that. You have certainly done your homework Pate. We can decrement each dogs’ daily treat number like this.”
Picture 9. The map function is applied to a list of treat numbers and each item on the list is subtracted 2.
> treatNumberList = [2,3,5,1,3]
> newTreatNumberList = map (-2) treatNumberList
> newTreatNumberList
=> [0,1,3,-1,1]
”You might have noticed that the fourth number that represents the number of treats, is now a negative one. This is bad. We cannot imagine there being a negative number of something can we? But maybe we can think that we need to gain more rewards in the future in order to reach zero and finally reach a positive number and get back to business of enjoying chicken jerky treats. We do not pay attention to this problem for now, but it is important to realize that our program could be still enhanced in many ways.“
“Thank you so much for your advice Selma”, replies Pate. “I would like to define a function that would favour good behaviour and disfavour bad behaviour. The function would give more treats for good behaviour and less treats for bad behaviour. The function could work in a way that it would decrement the daily treat number by one if one had run after a rabbit more than twice within a week without permission. Could we build such a function with this information, and what would the function look like Selma?”
“You seem to be excited about these functions and I do not wonder. A smart dog can do all sorts of things with these functions of higher order. First, we need to know how many times one has chased a rabbit without a permission within a week. Let’s list how many times each dog has chased a rabbit without a permission within a week.”
Selma, 4 times
Topi, 2 times
Repa, 2 times
Motti, 9 times
Pate, 2 times.
The hand-written list can also be represented by a list [4,2,2,9,2].
Now we only have a simple task left. We need to decrement the number of the treats if a dog has chased a rabbit more than twice within a week. We solve the problem in the following way.
First, we create a list of pairs where the first item of the pair (fst) represents the current number of treats and the second item of the pair (snd) represents the number of rabbit chasing events. Because each dog is represented by a pair like this, we need a list with 5 such pairs.
We can us the zip function to create a list of pairs. The Zip function is fed with treatNumberList and rabbitChasingList. Zip function will produce a list of pairs. The first item of each pair (fst) of the list is the number of treats and the second item of each pair (snd) of the list is the number of how many times the dog has chased a rabbit within a week.
Zip function works like a real zipper. We take items from left and right and put them together to form a tuple such as (4,5) and so forth. The types of values within the tuple could be everything but each tuple on the list must be of the same type. That is why tuples such as (10,3) and (10, ”Pate”) cannot exist on the same list.
This is how the zipper is being zipped. We can also unzip the tuples if we want to. Two halves become one once the zipper is closed.
Picture 10. Two lists are zipped into one by the zip function.
> zip [2,3,5,1,3] [4,2,2,9,2]
=> [(2,4),(3,2),(5,2),(1,9),(3,2)]
Now we would only need to define a function that produced a new treat number list that was based on the number of rabbit chasing events.
As we remember, map function transforms a list items and produces a new list. The map function handles the first list item (2,4). If the list item (pair) is represented by x, the latter item of the pair is represented by snd x. The first item of the pair is represented by fst x. Fst is a function that evaluates to the value of the first item of the tuple when the function is applied to a tuple. Snd in turn is a function that evaluates to the second item of the tuple when the function is applied to a tuple.
In order to find out if a dog has chased a rabbit more than twice in a week, we need to check if the second item of the tuple is greater than 2. When we combine this idea with what we already know about the guards we can end up with the following function named rule.
If that happens to be the case we should decrement the number of treats by one. This could be represented by a function:
rule x — x is one pair!
|snd x>2 = fst x-1
|otherwise = fst x
Rule function is fed with a pair. If the second item of the pair (representing the number of rabbit chasing events) is greater than 2, the function produces the number of treats minus one, which is represented by fst x-1. If the number of rabbit chasing events is less or equal to 2, the function produces the current number of treats for a dog, which is represented by fst x. Let’s look at the kind of functions we end up with. This is depicted in the next picture.”
Picture 11. The rule function is in a decisive role when the list of pairs is transformed into a simple list.
treatNumberList=[2,3,5,1,3]
rabbitChasingList=[4,2,2,9,2]
treatsAndChasesList=zip treatNumberList rabbitChasingList
rule x
|snd x>2 = fst x-1
|otherwise = fst x
newTreatNumberList = map rule treatsAndChasesList
”Now that we apply map function to its arguments rule and newTreatNumberList we get to know the new treat numbers for each dog. The map function will apply the rule function on each item of the treatsAndChasesList list.
> newTreatNumberList
=> [1,3,5,0,3]
”If we recall the order of the dogs on the list we can come up with the following table.”
Selma, 1
Topi, 3
Repa, 5
Motti, 0
Pate, 3.
”It looks like Selma’s and Motti’s treat numbers have been made smaller, because they have been chasing rabbits without permission. Let’s look at another picture to still deepen our understanding of how things work as a whole. To make things more visible, I added the names of the dogs to the picture in order to better depict the lists which are fed to the function. We can depict our new function with one picture.
Picture 12. The lists can be given names and we can reuse them everywhere in our program.
One the left of the picture you can see the zip function which is fed to the map function. The right side of the picture means the same as the left side of the picture. On the right side, functions and arguments are given proper names.
Map function applies the rule function to each pair of the list and finally we have a new list that depicts the new number of treats per day for each dog. The wisdom of the rule function is that once it is fed with a pair, it knows to transform the pair into a new value. Where the filter function produces a new list, which is either empty or contains at most the same number of items as the original list, the map function always produces a list which with the same number of items as the original list.“
“That is quite a function!” says Pate. “But we still have not solved the problem that was presented in the previous chapter. We were supposed to define a function that could produce the distribution of the big bag of treats without the need to explicitly define the functions that would count the number of each treat. That is what I call automation data processing. Could you tell me how to define such a function Selma?“
”I sure will. It is really simple. First, a nub function is applied to the treatList. This will produce a list where each treat appears only once. Then we apply the map function to the treatSet list. The treatSet depicts the classification or distribution. In addition to the treatSet the map function is fed with the function that is applied to each item of the treatSet. For each item of the treatSet, we will find out how many times the item is present in the treatList.
Now, we only need to figure out how to define the function that would be fed to the map function in order to solve the problem. The new function would be fed with a treat’s name and it would figure out the number of the treat on the treatList. The function could be named counter and we could define it this way. X depicts the name of the treat.
counter x=length(filter(==x)treatList))
Now that we have defined the counter function, we can write the rest of the functions that use the counter function.
treatList = [”chicken jerky treat”,” chicken jerky treat ”,”dog chocolate drop”, ”marrowbone”]
treatSet=nub treatList
treatDistribution=map counter treatSet
> treatDistribution
=> [2,1,1]
Let’s look at this step-by-step. The TreatList is [”chicken jerky treat”,” chicken jerky treat ”,”dog chocolate drop”, ”marrowbone”]. The treatSet is produced by applying the nub function to the treatList. In more detail [” chicken jerky treat ”,”dog chocolate drop”, ”marrowbone”] is produced by feeding the nub function with [”chicken jerky treat”,” chicken jerky treat ”,”dog chocolate drop”, ”marrowbone”].
Finally, the treatSet is fed to the map function and we let the counter function to do its job and find out how many times each treat is present in the treatList.
Map and filter functions are among the most well-known functions in functional programming and many imperative languages such as Python and JavaScript, provide the functions, too.
Instead of using map and filter functions to solve the treat distribution problem, we could use the fold function. Fold is the last higher-order function of the book and we need another chapter for dealing with it. But now it is time to forget about the function for a while and reward ourselves with 2 tasty chicken jerky treats, one each.”
“Sounds like a plan”, replies Pate as he gets his teeth on the treat.
Chapter 8. Fold function
”Did you know that modern data processing is not only the changing of the daily number of treats according to how the dogs behave? Often there is a need to come up with all sorts of summaries of data. One such summary is the distribution of different kinds of treats of the treatList.
The treatList has all the information we need in order to come up with the distribution, but it takes several function to define such functions. There is a better solution. We can use the fold function. Let’s see how map and filter functions can be replaced by the fold function.”
”Fold function sounds like a many fold thing”, says Pate.
”That’s what it is”, replies Selma. “Let’s think that your eurasier friend Topi has just received the following diploma from the dog school having passed the first grade. The skills are divided into 3 groups: hunting, fun activities and other skills.
Hunting
Rabbit chasing 9
Moose tracking 8
Bird fetching 8
Fun activities
Rolling in the snow 10
Digging of flowerbeds 10
Other activities
Guarding of the backyard 9
Finding a hidden bone 7
Chasing one’s own tail 9
Howling at the Moon 8
In order to compare the scores groupwise, we need to calculate the group scores for each dog. What kind of information would we need to come up with such a calculation?” asks Selma.
”Well at least we need to know which skill falls into which category. Therefore we need some kind of classification and maybe a function, a classifier, that could classify the data. We could use pairs. The first item of the pair could represent a skill and the second item of the pair could represent a category the skill falls into. A simple tuple with a pair of two values can be used to solve the problem data type wise. Could we define the classification this way?” asks Pate and shows some code.
classification=[(”Rabbit chasing”,”Hunting”),
(”Moose tracking”,”Hunting”),
(”Bird fetching”,”Hunting”),
(”Rolling in the snow”,”Fun activities”),
(”Digging of the flowerbeds”,”Fun activities”),
(”Guarding of the backyard”, ”Other activities”),
(”Finding a hidden bone”,”Other activities”),
(”Chasing one’s own tail”,”Other activities”),
(”Howling at the moon”,”Other activities”)]
””We sure can”, replies Selma. ”There they are! Now we only need to make the diploma such that it only shows the grades per category. Could you write such a program Pate?”
”Well, I can always try. This is how I would turn the ideas into a program and this is what Topi’s diploma could look like”, replies Pate.
topisDiploma = [(”Rabbit chasing”,9),
(”Moodes tracking”,8),
(”Bird fetching”,8),
(”Rolling in the snow”,10),
(”Digging of the flowerbeds”,10),
(”Guarding of the backyard”,9),
(”Finding a hidden bone”,7),
(”Chasing one’s own tail”,9),
(”Howling at the moon”,8)]
”That looks really good”, says Selma. “Now we only need to create a program which can count the sums of the grades for each category. Data types is not of our interest in this book, but for the fold function we will define one like this.”
data CategorySums = CategorySums {hunting::Int, fun::Int, other::Int}
”Now everything that we need to define is defined. The only thing to work on is to think the kind of functions we might need in order to get the grades categorized and category sums counted. Let me tell you how you could approach the problem Pate”, says Selma.
”Ok. If I can solve one more problem with you, will you promise to reward me with an extra tasty chicken jerky treat?” asks Pate.
”Absolutely”, replies Selma. ”Let’s see how the problem could be solved”, says Selma.
sumsPerCategory = foldr (\x acc->case (classify (fst x) of
”Hunting” -> acc {hunting=(hunting acc)+snd x}
”Fun activities” -> acc {fun=(fun acc)+snd x}
”Other activities” -> acc {other=(other acc)+snd x})
CategorySums {hunting=0, yard=0, other=0} topisDiploma
”This piece of code has a lot of new things such as data types we are not yet aware of. But for now we do not need to worry about all the details. We are happy to get the big picture right. The sumsPerCategory function is based on the foldr function. Foldr is fed with three arguments.
First, the foldr is fed with Topi’s grades. It is the last argument of the three and is represented by topisDiploma. The second argument of the foldr function is the initial value for CategorySums. This value contains the initial values for each category {hunting=0, yard=0, other=0}. The name CategorySums of the data type reveals the kind of data we will be dealing with – three named fields that seem to be initialized to zeros. The third argument to the right of the foldr function name is the processing function itself:
(\x acc->case (classify (fst x) of
”Hunting” -> acc {hunting=(hunting acc)+snd x}
”Fun activities” -> acc {fun=(fun acc)+snd x}
”Other activities” -> acc {other=(other acc)+snd x})
The function above processes each item of the topisDiplloma list and reduces the list into a summary, the CategorySums.
What will happen when the sumsPerCategory function is evaluated and the arguments fed to the function are processed? How does the function work?
The function starts to process the first item of topisDiploma list. The function will explore the item of the pair that represents the skill. Remember that the grades are defined by (skill, grade) tuples. If the skill happens to be hunting, the hunting field of our CategorySums datatype will be transformed into a new value which will be the old value added by the value that is found in topisDiploma. In order to deal with the grade value of the tuple x, we use the snd function. This way we are handed the second item of the tuple and we can add it to the current sum of hunting related grades. To obtain the current value of the hunting related grades we apply hunting to the acc to extract the hunting value from the structured data type.
acc {hunting=(hunting acc)+snd x}
All this works because acc is the name of the value of type CategorySums. This value contains three integers. These three integer fields represent the sums of different categories of hunting, fun activities and other activities and depict the sums of each category which are accumulated while the function is evaluated. To name the accumulator argument as acc or something similar is a good convention because it reminds us that something is accumulated during the evaluation of the sumsPerCategory function.
As data that is accumulated during the process, the further we are in the evaluation process the more information will be packed in acc. Acc is recreated every time topisDiploma list is found a grade that is not yet categorized. The new category sum value is created by adding the grade found in topisDiploma to the current sum of the respective category. The function will traverse all the items of topisDiploma and produces a value of type CategorySums that holds the sums for each category.
In order to work the sumsPerCategory function needs to find the categories that correspond to the skills found in topisTodistus. Otherwise the grades cannot be grouped. Therefore I defined a small function classify that is fed with skill and a function that can produce the corresponding category.
(\x acc->case (classify (fst x)…
X represent an item of topisDiploma and it is a tuple of skill and grade. Therefore, the skill item can be extracted from the tuple by the fst function. Once the skill part of the tuple is extracted it fed to to the classify function which looks like this.
classify skill = snd(head(filter(\z-> (fst z)==skill) classification))
Classify is a simple function that is fed with a skill and a classification, and it will produce a category. The classification has information on how different skills are mapped to different categories. Also, the function body has a filter function that picks the category that correspond to the skill in question. (filter(\z-> (fst z)==skill). Because the filter function always produces a list, we need to pick the first item of the list by using the head function. Then we use the snd function to pick the second item of the tuple and finally we have a category that corresponds to the skill that was fed to the function in the first place. If we now ask the interpreter to evaluate the function like this
> sumsPerCategory
we get the following reponse
=> CategorySums {hunting = 25, fun = 20, other = 33}
We saw a strange looking piece of code like (\z->… in many places. This kind of expressions refer to nameless or anonymous functions. In programming terms, the functions were defined lambda expressions.
The last chapter of the book by no means the most challenging of them all, but practice makes the master”, says Selma. “Now that you know some basic concepts you can start your own learning process. Internet is full of useful resources on functional programming and programming in general.
A good understanding of lambdas and basic higher order functions are not only useful in learning functional languages like Haskell, ML, Clojure, Elm, Racket, ML, Idris and many others, but they are also useful for learning to write high quality software in any programming language.
Many languages contain numerous functional concepts, the most obvious being the higher order functions map, filter and fold (reduce) to manipulate arrays or array like data types. Functional features have been introduced into many popular programming languages such as JavaScript, C#, Python, Scala, PHP, Ruby, Kotlin, TypeScript, Java, C++ and many others.
Now it is time for chicken jerky treats! Let’s go and see our master and ask for two super-hyper-extra tasty treats as a reward for studying hard. As the Beatles put it, we have been working like dogs. Dogs do not live by functions alone!”, says Selma.
”You are dead right. In treats we trust!”, says Pate.
As the day passed into the evening, the dogs fell asleep and in their dreams they wondered if a list of chicken jerky treats could be a never ending and would last ad infinitum.
Recommended reading
For the ones that need to introduce themselves to the topic
Lipovača, Miran 2011: Learn You a Haskell for Great Good!, https://www.learnyouahaskell.com
For the ones interested in the theory behind
Milewski, Bartosz 2014: Category theory for programmers, https://bartoszmilewski.com/2014/10/28/category-theory-for-programmers-the-preface
For the ones who want to read the top-notch Haskell educator’s book with exercises
Hutton, Graham 2016: Programming in Haskell, 2nd Edition, https://www.cs.nott.ac.uk/~pszgmh/pih.html
”List in, list out, this is cool, there is no doubt”, says Pate.
Programming is considered an important skill in Finnish schools. It was added to the national curriculum two years ago as Finland reformed the national core curricula at all levels of education.
Programming could be a hobby, but it could turn into one’s profession later in life. Functional programming paradigm suites problems that are data processing intensive.
An Irish wheaten terrier Pate is taking his first steps in programming Haskell and will be guided by a bichpoo Selma in this chicken jerky flavoured book.
This book suites anyone who wants to learn some of the most essential ideas of functional programming explained in a doglike way.